Rumus Rumus Diferensial
Persamaan diferensial adalah persamaan matematika untuk fungsi satu variabel atau lebih, yang menghubungkan nilai fungsi itu sendiri dan turunannya dalam berbagai orde. Persamaan diferensial memegang peranan penting dalam rekayasa, fisika, ilmu ekonomi dan berbagai macam disiplin ilmu alin.Persamaan diferensial muncul dalam berbagai bidang sains dan teknologi, bilamana hubungan deterministik yang melibatkan besaran yang berubah secara kontinu (dimodelkan oleh fungsi matematika) dan laju perubahannya (dinyatakan sebagai turunan) diketahui atau dipostulatkan. Ini terlihat misalnya pada mekanika klasik, di mana gerakan sebuah benda diperikan oleh posisi dan kecepatannya terhadap waktu. Hukum Newton memungkinkan kita mengetahui hubungan posisi, kecepatan, percepatan dan berbagai gaya yang bertindak terhadap benda tersebut, dan menyatakannya sebagai persamaan diferensial posisi sebagai fungsi waktu. Dalam banyak kasus, persamaan diferensial ini dapat dipecahkan secara eksplisit, dan menghasilkan hukum gerak.
Contoh pemodelan masalah dunia nyata menggunakan persamaan diferensial adalah penentuan kecepatan bola yang jatuh bebas di udara, hanya dengan memperhitungkan gravitasi dan tahanan udara. Percepatan bola tersebut ke arah tanah adalah percepatan karena gravitasi dikurangi dengan perlambatan karena gesekan udara. Mencari kecepatan sebagai fungsi waktu mensyaratkan pemecahan sebuah persamaan diferensial.
1.Definisi Turunan
Misalkan y adalah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x dinotasikan dengan :
2.Rumus- Rumus Turunan Dengan menggunakan definisi turunan dapat diturunkan sejumlah rumus tentang turunan, yaitu:
* Jika dengan C dan n konstanta real, maka :
dengan C dan n konstanta real, maka : 

* Jika y = C dengan

* Jika y = f(x) + g(x) maka

* Jika y = f(x).g(x) maka

*

*
3. Turunan Kedua
Turunan kedua y = f(x) terhadap x dinotasikan dengan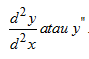 . Turunan kedua diperoleh dengan menurunkan turunan pertama.
. Turunan kedua diperoleh dengan menurunkan turunan pertama.
Contoh :

4. Penggunaan Turunan * Menentukan gradien garis singgung kurva
Misal garis g menyinggung kurva y = f (x) dititik (a,f(a)) maka gradien g adalah :
Contoh :
Tentukan gradien garis singgung kurva
Jawab :

Gradien garis singgung kurva dititik (1,4) adalah
* Menentukan interval naik dan turun

Interval yang memenuhi dan dan ditentukan denggan menggambarkan garis bilangan dari f '(x) .
dan ditentukan denggan menggambarkan garis bilangan dari f '(x) .
Contoh :
Tentukan interval fungsi naik dan turun dari
Jawab :



* Menentukan nilai maksimum dan minimum
Nilai maksimum dan minimum fungsi sering disebut nilai ekstrim atau nilai stasioner fungsi tersebut. Nilai ekstrim dari fungsi y = f(x) diperoleh pada f '(x) = 0
Contoh :
Jika maka nilai stasionernya adalah :
maka nilai stasionernya adalah :


*Fungsi maksimum pada x=-2, maka nilai balik maksimumnya :

* Fungsi minimum pada x=4, maka nilai balik minimumnya :

3. TURUNAN FUNGSI TRIGONOMETRI
Rumus-rumus Turunan fungsi Trigonometri adalah:
Misalkan y adalah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x dinotasikan dengan :

2.Rumus- Rumus Turunan Dengan menggunakan definisi turunan dapat diturunkan sejumlah rumus tentang turunan, yaitu:
* Jika
 dengan C dan n konstanta real, maka :
dengan C dan n konstanta real, maka : 

* Jika y = C dengan


* Jika y = f(x) + g(x) maka


* Jika y = f(x).g(x) maka


*


*

3. Turunan Kedua
Turunan kedua y = f(x) terhadap x dinotasikan dengan
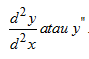 . Turunan kedua diperoleh dengan menurunkan turunan pertama.
. Turunan kedua diperoleh dengan menurunkan turunan pertama.Contoh :

4. Penggunaan Turunan * Menentukan gradien garis singgung kurva
Misal garis g menyinggung kurva y = f (x) dititik (a,f(a)) maka gradien g adalah :

Contoh :
Tentukan gradien garis singgung kurva

Jawab :

Gradien garis singgung kurva dititik (1,4) adalah

* Menentukan interval naik dan turun

Interval yang memenuhi dan
 dan ditentukan denggan menggambarkan garis bilangan dari f '(x) .
dan ditentukan denggan menggambarkan garis bilangan dari f '(x) .Contoh :
Tentukan interval fungsi naik dan turun dari

Jawab :



* Menentukan nilai maksimum dan minimum
Nilai maksimum dan minimum fungsi sering disebut nilai ekstrim atau nilai stasioner fungsi tersebut. Nilai ekstrim dari fungsi y = f(x) diperoleh pada f '(x) = 0
Contoh :
Jika
 maka nilai stasionernya adalah :
maka nilai stasionernya adalah :

*Fungsi maksimum pada x=-2, maka nilai balik maksimumnya :

* Fungsi minimum pada x=4, maka nilai balik minimumnya :

3. TURUNAN FUNGSI TRIGONOMETRI
Rumus-rumus Turunan fungsi Trigonometri adalah:
Jawab:
Jawab:







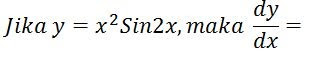


Tidak ada komentar:
Posting Komentar