Algoritma Pembuatan Garis
Algoritma pembuatan garis lurus vertikal dan horisontal relatif mudah, tetapi bila garis tersebut miring, maka algoritma menjadi sulit.
Misalkan : Line (1,3,8,5).
m = (y2-y1)/(x2-x1) = (5-3)/(8-1) = 2/7
c = y1 � m.x1 = 3 � 2/7.1 = 19/7
y = 2/7.x + 19/7
Algoritma garis Bresenham adalah suatu algoritma yang menentukan untuk membentuk pendekatan dekat dengan garis lurus antara dua poin yang diberikan . Hal ini biasanya digunakan untuk menggambar garis pada layar komputer , karena hanya menggunakan penambahan integer, pengurangan dan pergeseran bit , yang semuanya beroperasi sangat murah dalam arsitektur komputer standar. Ini adalah salah satu algoritma paling awal dikembangkan di bidang komputer grafis . Sebuah ekstensi kecil dengan algoritma asli juga berhubungan dengan lingkaran gambar .Sedangkan algoritma seperti algoritma Wu juga sering digunakan dalam grafis komputer modern karena mereka dapat mendukung antialiasing , kecepatan dan kesederhanaan algoritma garis Bresenham berarti bahwa masih penting . Algoritma ini digunakan dalam perangkat keras seperti plotters dan dalam chip grafis dari kartu grafis modern . Hal ini juga dapat ditemukan di banyak perangkat lunak perpustakaan grafis . Karena algoritma ini sangat sederhana , sering dilaksanakan baik dalam firmware atau perangkat keras grafis dari kartu grafis modern .Label " Bresenham " digunakan hari ini untuk seluruh keluarga algoritma memperluas atau memodifikasi algoritma Bresenham itu asli . Lihat referensi lebih lanjut di bawah ini.
Algoritma ini dikembangkan oleh Jack Elton Bresenham pada tahun 1962 di IBM. Pada tahun 2001 Bresenham menulis:
Saya bekerja di laboratorium komputasi di IBM di San Jose pengembangan lab. Calcomp plotter terlanjur lekat dengan IBM 1401 melalui 1407 mesin ketik konsol. [Algoritma] pada penggunaan produksi oleh musim panas tahun 1962, mungkin satu bulan atau lebih awal. Program di hari-hari bebas dipertukarkan antara perusahaan sehingga Calcomp (Jim Newland dan Calvin Hefte) memiliki salinan. Ketika aku kembali ke Stanford pada musim gugur tahun 1962, aku meletakkan sebuah salinan di Perpustakaan Pusat comp Stanford. Deskripsi gambar garis rutin diterima untuk presentasi pada 1963 ACM Konvensi Nasional di Denver, Colorado. Ini adalah tahun di mana ada proses yang diterbitkan, hanya agenda pembicara dan topik dalam masalah komunikasi dari ACM. Seseorang dari jurnal sistem IBM bertanya setelah saya membuat presentasi saya jika mereka bisa menerbitkan karya. Dengan senang hati saya setuju, dan mereka dicetak pada tahun 1965.
Algoritma Bresenham yang kemudian diubah untuk menghasilkan lingkaran, dihasilkan algoritma yang kadang-kadang dikenal sebagai "Bresenham's lingkaran algoritma" atau titik tengah lingkaran algoritma.
Konvensi Umum akan digunakan:
- bagian kiri adalah (0,0) sedemikian rupa sehingga piksel koordinat meningkatkan di kanan dan bawah arah (misalnya yang pixel pada (7,4) berada langsung di atas pixel pada (7,5)), dan
- bahwa pusat pixel memiliki integer koordinat.
Endpoint baris piksel pada (x0, y0) dan (x1, y1), di mana koordinat pertama pasangan kolom dan yang kedua adalah baris.
Algoritma akan disajikan pada awalnya hanya untuk octant di mana segmen pergi ke bawah dan ke kanan (x0 = x1 dan y0 = y1), dan proyeksi horisontal yang  lebih lama dari proyeksi vertikal
lebih lama dari proyeksi vertikal  (garis telah negatif lereng yang nilai absolut adalah kurang dari 1). Dalam octant ini, untuk setiap kolom x antara
(garis telah negatif lereng yang nilai absolut adalah kurang dari 1). Dalam octant ini, untuk setiap kolom x antara  dan
dan  , ada satu baris y (dihitung oleh algoritma) mengandung piksel baris, sementara setiap baris antara
, ada satu baris y (dihitung oleh algoritma) mengandung piksel baris, sementara setiap baris antara  dan
dan  mungkin berisi beberapa raster piksel.
mungkin berisi beberapa raster piksel.
Algoritma Bresenham's memilih integer y sesuai dengan pusat pixel yang terdekat dengan ideal (pecahan) y untuk sama x; pada kolom berturut-turut y dapat tetap sama atau meningkatkan dengan 1. Persamaan umum dari line melewati Endpoint diberikan oleh:
Karena kita tahu kolom x, dengan pixel baris, y, diberikan oleh pembulatan ini jumlah ke integer terdekat:
Lereng  tergantung pada akhir koordinat hanya dan dapat precomputed, dan ideal y untuk nilai-nilai integer berturut-turut x bisa dihitung mulai dari
tergantung pada akhir koordinat hanya dan dapat precomputed, dan ideal y untuk nilai-nilai integer berturut-turut x bisa dihitung mulai dari  dan berulang kali menambahkan lereng.
dan berulang kali menambahkan lereng.
Dalam prakteknya, algoritma dapat melacak, bukan nilai-nilai y mungkin besar, nilai kesalahan kecil antara -0.5 dan 0,5: jarak vertikal antara bulat dan nilai-nilai tepat y untuk saat ini x. Setiap waktu x meningkat, kesalahan meningkat sebesar lereng; Jika memang melebihi 0,5, rasterization y meningkat sebesar 1 (garis terus di bawah baris berikutnya raster) dan kesalahan decremented oleh 1.0.
Dalam berikut palsu sampel
plot(x,y) plot titik dan abs mengembalikan nilai absolut 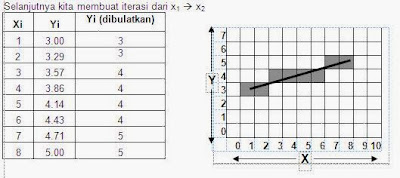
Tidak ada komentar:
Posting Komentar